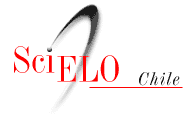Shrinkage effect on radial and tangential direction stresses in cylindrical wood pieces of Pinus taeda
DOI:
https://doi.org/10.22320/s0718221x/2025.28Keywords:
Anisotropic elasticity, compression wood, Lekhnitskii´s coefficients, wood shrinkageAbstract
Shrinkage is a key factor in generating internal stresses and deformations within wood structures, especially due to the anisotropic nature of wood, which causes direction-dependent stress responses and must be considered to accurately predict the mechanical behaviour of cylindrical elements. However, its influence on the stress distribution in cylindrical wood elements remains insufficiently explored. This study addresses this gap by formulating a theoretical model to evaluate the development of internal stresses resulting from the shrinkage of wood specimens.
Shrinkage was determined based on the stress–strain relationship of a cylindrical piece of wood, in the absence of external forces, within a cylindrical coordinate system. Due to its radial symmetry, the displacement field is a function of the radius, and the angular displacement is null. Assuming constant longitudinal strains, the strain components can be described as a function of Lekhnitskii’s reduced strain coefficients and the associated coefficient, denoted by k, where the coefficients depend on the material's elastic properties. Thus, the governing equation of the problem becomes a function of the strain coefficients and, consequently, of shrinkage.
To demonstrate the effects of shrinkage and to show how stresses in the radial and tangential directions are influenced, the elastic coefficients of the wood species Pinus taeda (loblolly pine) were experimentally obtained, and the coefficient k was determined. Overall, the results emphasise the importance of considering shrinkage and anisotropy when evaluating radial and tangential stresses, as well as radial displacements, in cylindrical wood elements.
Downloads
References
ABNT. 2022a. Projeto de estruturas de madeira – Parte 1: Critérios de dimensionamento. ABNT NBR 7190-1. ABNT: Rio de Janeiro, Brasil.
ABNT. 2022b. Projeto de estruturas de madeira – Parte 2: Métodos de ensaio para classificação visual e mecânica de peças estruturais de madeira. ABNT NBR 7190-2. ABNT: Rio de Janeiro, Brasil.
ABNT. 2022c. Projeto de estruturas de madeira – Parte 3: Métodos de ensaio para corpos de prova isentos de defeitos para madeiras de florestas nativas. ABNT NBR 7190-3. ABNT: Rio de Janeiro, Brasil.
Bodig, J.; Jayne, B.A. 1982. Mechanics of wood and wood composites. Krieger Publishing Company: Florida, USA. ISBN 9780898745370. 712p.
Corradi, M.; Adelaja, I.O.; Borri, A. 2019. Repair and reinforcement of historic timber structures with stainless steel. Metals 9(1). e106. https://doi.org/10.3390/met9010106
European Committee for Standardization. 2010. Structural round timber – Requirements for visual grading of softwood. EN 14229. CEN: Brussels, Belgium. https://www.en-standard.eu/eurocodes
Fridley, K.J.; Tang, R.C. 1993. Modelling three-dimensional distortion of wood due to anisotropic shrinkage. Mathematical and Computer Modelling 17(9): 23–30. https://doi.org/10.1016/0895-7177(93)90014-P
Gopu, V.K.A.; Goodman, J.R. 1974. Analysis of double-tapered pitched and curved laminated beam section. Wood Science 7(1): 52–60.
Halsenman, D.; Littlefield, B. 1999. Matlab 5 – Versão do estudante: guia do usuário. Makron Books: São Paulo, Brasil. ISBN 9788534606566. 320p.
Hashin, Z. 1967. Plane anisotropic beams. Journal of Applied Mechanics 34(2): 257-262. https://doi.org/10.1115/1.3607676
Kongyang, C.; Hongxing, Q.; Menglin, S.; Frank, L. 2019. Experimental and numerical study of moisture distribution and shrinkage crack propagation in cross section of timber members. Construction and Building Materials 221: 219–231. https://doi.org/10.1016/j.conbuildmat.2019.05.191
Hsu, N.N.; Tang, R.C. 1974. Internal stresses in wood logs due to anisotropic shrinkage. Wood Science 7(1): 43–51.
Lekhnitskii, S.G. 1981. Theory of elasticity of an anisotropic body. Mir Publishers: Moscow, Russia. ISBN 9780828522409. 320p.
Malvern, L.E. 1969. Introduction to the mechanics of a continuous media. Prentice-Hall International: London, UK. ISBN 9780134876030. 713p.
Mascia, N.T. 2015. Análise de tensões e deslocamentos em peças cilíndricas de madeira devido à retração. Matéria 20(1): 32–46. https://doi.org/10.1590/S1517-707620150001.0007
Mascia, N.T.; Nicolas, E.A. 2013. Determination of Poisson’s ratios in relation to fiber angle of a tropical wood species. Construction and Building Materials 41: 691–696. https://doi.org/10.1016/j.conbuild-mat.2012.12.014
Mustefaga, E.C.; Hillig, E.; Tavares, E.L.; Sozim, P.C.L.; Rusch, F. 2019. Caracterização físico-mecânica da madeira juvenil de Pinus. Scientia Forestalis 47(123): 472–481. https://doi.org/10.18671/scifor.v47n123.09
O’Regan, P.J.; Woeste, F.E. 2002. Withdrawal strength of punched metal tooth plates in red oak end grain. Forest Products Journal 52(10): 82–88.
Saliklis, E. 1992. A nonlinear constitutive model of paperboard. PhD Thesis. University of Wisconsin-Madison. 246p.
Svensson, S.; Toratti, T. 2002. Mechanical response of wood perpendicular to grain when subjected to changes of humidity. Wood Science and Technology 36: 145–156. https://doi.org/10.1007/s00226-001-0130-4
Ting, T.C.T. 1996. Anisotropic elasticity: theory and applications. Oxford University Press: New York, USA. ISBN 9780195074478. 573p.
Trianoski, R.; Matos, J.M.; Iwakiri, S.; Prata, J.G. 2013. Avaliação da estabilidade dimensional de espécies de Pinus tropicais. Floresta e Ambiente 20(3): 398–406. http://dx.doi.org/10.4322/floram.2012.071
Vilela, R.T.; Mascia, N.T. 2021. Avaliação de propriedades mecânicas da madeira de Pinus taeda provenientes de placas de cross-laminated timber. Ambiente Construído 21(4): 89–110. https://doi.org/10.1590/s1678-86212021000400560
Ylinen, A.; Jumppanen, P. 1967. Theory of the shrinkage of wood. Wood Science and Technology 1(4): 241–252.
Zenid, G.J. 2003. Madeira: uso sustentável na construção civil. Instituto de Pesquisas Tecnológicas (IPT): São Paulo, Brasil. https://madeiras.ipt.br/madeira-uso-sustentavel-na-construcao-civil/
Downloads
Published
How to Cite
Issue
Section
License

This work is licensed under a Creative Commons Attribution 4.0 International License.
Los autores/as conservarán sus derechos de autor y garantizarán a la revista el derecho de primera publicación de su obra, el cuál estará simultáneamente sujeto a la Licencia de Reconocimiento de Creative Commons CC-BY que permite a terceros compartir la obra siempre que se indique su autor y su primera publicación esta revista.